| RAP,DAP |
D |
geocentric apparent ![$[\,\alpha,\delta\,]$](img3.gif) (radians) (radians) |
|---|
| AOPRMS |
D(14) |
star-independent apparent-to-observed parameters: |
| (1) |
|
geodetic latitude (radians) |
| (2,3) |
|
sine and cosine of geodetic latitude |
| (4) |
|
magnitude of diurnal aberration vector |
| (5) |
|
height (metres) |
| (6) |
|
ambient temperature (degrees K) |
| (7) |
|
pressure (mB) |
| (8) |
|
relative humidity (0-1) |
| (9) |
|
wavelength (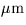 ) ) |
| (10) |
|
lapse rate (degrees K per metre) |
| (11,12) |
|
refraction constants A and B (radians) |
| (13) |
|
longitude + eqn of equinoxes +
``sidereal 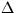 UT'' (radians) UT'' (radians) |
| (14) |
|
local apparent sidereal time (radians) |
