


Next: Precession and Nutation
Up: EXPLANATION AND EXAMPLES
Previous: Using vectors
SLALIB has routines to perform transformations
of celestial positions between different spherical
coordinate systems, including those shown in the following table:
| system |
symbols |
longitude |
latitude |
x-y plane |
long. zero |
RH/LH |
|---|
| horizon |
- |
azimuth |
elevation |
horizontal |
north |
L |
| equatorial |
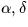 |
R.A. |
Dec. |
equator |
equinox |
R |
| local equ. |
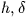 |
H.A. |
Dec. |
equator |
meridian |
L |
| ecliptic |
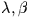 |
ecl. long. |
ecl. lat. |
ecliptic |
equinox |
R |
| galactic |
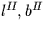 |
gal. long. |
gal. lat. |
gal. equator |
gal. centre |
R |
| supergalactic |
SGL,SGB |
SG long. |
SG lat. |
SG equator |
node w. gal. equ. |
R |
Transformations between ![$[\,h,\delta\,]$](img29.gif) and
and ![$[\,Az,El~]$](img28.gif) can be performed by
calling
sla_E2H
and
sla_H2E,
or, in double precision,
sla_DE2H
and
sla_DH2E.
There is also a routine for obtaining
zenith distance alone for a given
can be performed by
calling
sla_E2H
and
sla_H2E,
or, in double precision,
sla_DE2H
and
sla_DH2E.
There is also a routine for obtaining
zenith distance alone for a given ![$[\,h,\delta\,]$](img29.gif) ,sla_ZD,
and one for determining the parallactic angle,
sla_PA.
Three routines are included which relate to altazimuth telescope
mountings. For a given
,sla_ZD,
and one for determining the parallactic angle,
sla_PA.
Three routines are included which relate to altazimuth telescope
mountings. For a given ![$[\,h,\delta\,]$](img29.gif) and latitude,
sla_ALTAZ
returns the azimuth, elevation and parallactic angle, plus
velocities and accelerations for sidereal tracking.
The routines
sla_PDA2H
and
sla_PDQ2H
predict at what hour angle a given azimuth or
parallactic angle will be reached.
and latitude,
sla_ALTAZ
returns the azimuth, elevation and parallactic angle, plus
velocities and accelerations for sidereal tracking.
The routines
sla_PDA2H
and
sla_PDQ2H
predict at what hour angle a given azimuth or
parallactic angle will be reached.
The routines
sla_EQECL
and
sla_ECLEQ
transform between ecliptic
coordinates and ![$[\,\alpha,\delta\,]$](img3.gif) ; there is also a routine for generating the
equatorial to ecliptic rotation matrix for a given date:
sla_ECMAT.
; there is also a routine for generating the
equatorial to ecliptic rotation matrix for a given date:
sla_ECMAT.
For conversion between Galactic coordinates and ![$[\,\alpha,\delta\,]$](img3.gif) there are
two sets of routines, depending on whether the
there are
two sets of routines, depending on whether the ![$[\,\alpha,\delta\,]$](img3.gif) is
old-style, B1950, or new-style, J2000;
sla_EG50
and
sla_GE50
are
is
old-style, B1950, or new-style, J2000;
sla_EG50
and
sla_GE50
are ![$[\,\alpha,\delta\,]$](img3.gif) to
to ![$[\,l^{I\!I},b^{I\!I}\,]$](img98.gif) and vice versa for the B1950 case, while
sla_EQGAL
and
sla_GALEQ
are the J2000 equivalents.
and vice versa for the B1950 case, while
sla_EQGAL
and
sla_GALEQ
are the J2000 equivalents.
Finally, the routines
sla_GALSUP
and
sla_SUPGAL
transform ![$[\,l^{I\!I},b^{I\!I}\,]$](img98.gif) to de Vaucouleurs supergalactic longitude and latitude
and vice versa.
to de Vaucouleurs supergalactic longitude and latitude
and vice versa.
It should be appreciated that the table, above, constitutes
a gross oversimplification. Apparently
simple concepts such as equator, equinox etc. are apt to be very hard to
pin down precisely (polar motion, orbital perturbations ...) and
some have several interpretations, all subtly different. The various
frames move in complicated ways with respect to one another or to
the stars (themselves in motion). And in some instances the
coordinate system is slightly distorted, so that the
ordinary rules of spherical trigonometry no longer strictly apply.
These caveats
apply particularly to the bewildering variety of different
![$[\,\alpha,\delta\,]$](img3.gif) systems that are in use. Figure 1 shows how
some of these systems are related, to one another and
to the direction in which a celestial source actually
appears in the sky. At the top of the diagram are
the various sorts of mean place
found in star catalogues and papers;
systems that are in use. Figure 1 shows how
some of these systems are related, to one another and
to the direction in which a celestial source actually
appears in the sky. At the top of the diagram are
the various sorts of mean place
found in star catalogues and papers;![[*]](foot_motif.gif) at the bottom is the
observed
at the bottom is the
observed ![$[\,Az,El~]$](img28.gif) , where a perfect theodolite would
be pointed to see the source; and in the body of
the diagram are
the intermediate processing steps and coordinate
systems. To help
understand this diagram, and the SLALIB routines that can
be used to carry out the various calculations, we will look at the coordinate
systems involved, and the astronomical phenomena that
affect them.
, where a perfect theodolite would
be pointed to see the source; and in the body of
the diagram are
the intermediate processing steps and coordinate
systems. To help
understand this diagram, and the SLALIB routines that can
be used to carry out the various calculations, we will look at the coordinate
systems involved, and the astronomical phenomena that
affect them.
Figure 1:
Relationship Between Celestial Coordinates
 |



Next: Precession and Nutation
Up: EXPLANATION AND EXAMPLES
Previous: Using vectors
SLALIB --- Positional Astronomy Library
Starlink User Note 67
P. T. Wallace
12 October 1999
E-mail:ptw@star.rl.ac.uk

![[*]](foot_motif.gif)
