| RAP,DAP |
D |
geocentric apparent ![$[\,\alpha,\delta\,]$](img3.gif) (radians) (radians) |
|---|
| DATE |
D |
UTC date/time (Modified Julian Date, JD-2400000.5) |
| DUT |
D |
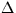 UT: UT1-UTC (UTC seconds) UT: UT1-UTC (UTC seconds) |
| ELONGM |
D |
observer's mean longitude (radians, east +ve) |
| PHIM |
D |
observer's mean geodetic latitude (radians) |
| HM |
D |
observer's height above sea level (metres) |
| XP,YP |
D |
polar motion ![$[\,x,y\,]$](img20.gif) coordinates (radians) coordinates (radians) |
| TDK |
D |
local ambient temperature (degrees K; std=273.155D0) |
| PMB |
D |
local atmospheric pressure (mB; std=1013.25D0) |
| RH |
D |
local relative humidity (in the range 0D0-1D0) |
| WL |
D |
effective wavelength (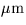 , e.g. 0.55D0) , e.g. 0.55D0) |
| TLR |
D |
tropospheric lapse rate (degrees K per metre,
e.g. 0.0065D0) |
