SLA_RCC - Barycentric Coordinate Time   

CALL:

D = sla_RCC (TDB, UT1, WL, U, V)

ACTION:

The relativistic clock correction TDB-TT, the difference between proper time on Earth and coordinate time in the solar system barycentric space-time frame of reference. The proper time is TT; the coordinate time is an implementation of TDB.

GIVEN:

TDB coordinate time (MJD: JD-2400000.5)

UT1 D universal time (fraction of one day)

WL D clock longitude (radians west)

U D clock distance from Earth spin axis (km)

V D clock distance north of Earth equatorial plane (km)

RETURNED:

sla_RCC TDB-TT (sec)

NOTES:

1.

TDB may be considered to be the coordinate time in the solar system barycentre frame of reference, and TT is the proper time given by clocks at mean sea level on the Earth.

2.

The result has a main (annual) sinusoidal term of amplitude approximately 1.66ms, plus planetary terms up to about 20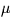$\mu$s, and lunar and diurnal terms up to 2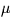$\mu$s. The variation arises from the transverse Doppler effect and the gravitational red-shift as the observer varies in speed and moves through different gravitational potentials.

3.

The argument TDB is, strictly, the barycentric coordinate time; however, the terrestrial proper time (TT) can in practice be used.

4.

The geocentric model is that of Fairhead & Bretagnon (1990), in its full form. It was supplied by Fairhead (private communication) as a Fortran subroutine. A number of coding changes were made to this subroutine in order match the calling sequence of previous versions of the present routine, to comply with Starlink programming standards and to avoid compilation problems on certain machines. On the supported computer types, the numerical results are essentially unaffected by the changes. The topocentric model is from Moyer (1981) and Murray (1983). During the interval 1950-2050, the absolute accuracy of the geocentric model is better than 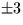$\pm3$ nanoseconds relative to direct numerical integrations using the JPL DE200/LE200 solar system ephemeris.

5.

The IAU definition of TDB is that it must differ from TT only by periodic terms. Though practical, this is an imprecise definition which ignores the existence of very long-period and secular effects in the dynamics of the solar system. As a consequence, different implementations of TDB will, in general, differ in zero-point and will drift linearly relative to one other.

REFERENCES:

1.

Fairhead, L. & Bretagnon, P., 1990. Astr.Astrophys. 229, 240-247.

2.

Moyer, T.D., 1981. Cel.Mech. 23, 33.

3.

Murray, C.A., 1983, Vectorial Astrometry, Adam Hilger.