- 1.
- ``Mean'' longitude and latitude are the (fixed) values for the site's location with respect to the IERS terrestrial reference frame; the latitude is geodetic. TAKE CARE WITH THE LONGITUDE SIGN CONVENTION. The longitudes used by the present routine are east-positive, in accordance with geographical convention (and right-handed). In particular, note that the longitudes returned by the sla_OBS routine are west-positive, following astronomical usage, and must be reversed in sign before use in the present routine.
- 2.
- XP and YP are the (changing) coordinates of the Celestial
Ephemeris Pole with respect to the IERS Reference Pole.
XP is positive along the meridian at longitude
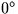 , and YP is positive along the meridian at longitude
, and YP is positive along the meridian at longitude
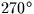 (i.e.
(i.e. 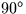 west). Values for XP,YP can
be obtained from IERS circulars and equivalent publications;
the maximum amplitude observed so far is about
west). Values for XP,YP can
be obtained from IERS circulars and equivalent publications;
the maximum amplitude observed so far is about
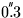 .
.
- 3.
- ``True'' longitude and latitude are the (moving) values for the site's location with respect to the celestial ephemeris pole and the meridian which corresponds to the Greenwich apparent sidereal time. The true longitude and latitude link the terrestrial coordinates with the standard celestial models (for precession, nutation, sidereal time etc).
- 4.
- The azimuths produced by sla_AOP and sla_AOPQK are with respect to due north as defined by the Celestial Ephemeris Pole, and can therefore be called ``celestial azimuths''. However, a telescope fixed to the Earth measures azimuth essentially with respect to due north as defined by the IERS Reference Pole, and can therefore be called ``terrestrial azimuth''. Uncorrected, this would manifest itself as a changing ``azimuth zero-point error''. The value DAZ is the correction to be added to a celestial azimuth to produce a terrestrial azimuth.
- 5.
- The present routine is rigorous. For most practical
purposes, the following simplified formulae provide an
adequate approximation:
ELONG = ELONGM+XP*COS(ELONGM)-YP*SIN(ELONGM) PHI = PHIM+(XP*SIN(ELONGM)+YP*COS(ELONGM))*TAN(PHIM) DAZ = -SQRT(XP*XP+YP*YP)*COS(ELONGM-ATAN2(XP,YP))/COS(PHIM)
An alternative formulation for DAZ is:
X = COS(ELONGM)*COS(PHIM) Y = SIN(ELONGM)*COS(PHIM) DAZ = ATAN2(-X*YP-Y*XP,X*X+Y*Y)
